Effective A/B Testing
Making money with statistics
Ben Tilly
Pictage
(These slides use S5. Click anywhere to continue or use the keyboard shortcuts.)
Contents
What is A/B Testing?
- Develop two versions of a page
- Randomly show different versions to users
- Track how users perform
- Evaluate (that's where statistics comes in)
- Use the better version
Why A/B test?

- A typical website converts 2% of visitors into customers
- People can't explain why they left
- Small changes can make a big difference
- How about +40%?
- Google believes it works, see Website Optimizer
What Can You A/B Test?

- Removing form fields
- Adding relevant form fields
- Marketing landing pages
- Different explanations
- Having interstitial pages
- Email content
- Any casual decisions you care about
A/B tests do not substitute for

- Talking to users
- Usability tests
- Acceptance tests
- Unit tests
- Thinking
What is the G-test?

- A method for comparing 2 data sets
- It was invented by Karl Pearson in 1900
- It is a close relative of the chi-square test
- It is our main method for evaluating A/B tests
- There are alternatives
Limitations of the G-test

- Only answers yes/no questions (but you pick the question)
- Only handles 2 versions (there is a workaround)
- Requires independence in samples
- Does not do confidence intervals
What to measure

- Start your A/B test
- Divide your users into groups A and B
- Decide whether each person did what you want
- Reduce your results to 4 numbers:
($a_yes, $a_no, $b_yes, $b_no)
Arrange your measurements
|
|
Scary Math Part 1 - Addition
|
|
Scary Math Part 2 - Expectations
|
|
Scary Math Part 3 - G-test
- A basic G-test term looks like this:
2 * $measured * log( $measured / $expected ) - Statisticians know its distribution very well
- It is connected to something called chi-square
- We will discuss chi-square later
- For now treat as magic
Scary Math Part 4 - Calculation
We have 4 measurements and 4 expectations. So we have 4 G-test terms. We add them:
my $g_test
= 2 * ( $a_yes * log( $a_yes / $e_a_yes )
+ $a_no * log( $a_no / $e_a_no )
+ $b_yes * log( $b_yes / $e_b_yes )
+ $b_no * log( $b_no / $e_b_no )
);
Scary Math Part 5: Interpretation
use Statistics::Distributions qw(chisqrprob); my $p = chisqrprob(1, $g_test);

- If the samples are all independent...
- and the measured values are all at least 10...
- and the real performance of A and B is the same...
- then
$p ≈ prob(G-test should be> $g_test) - If
$pis "small", conclude #3 likely wrong
How Small Is "Small"?
- Increased certainty needs a larger sample
- You'd have to be unlucky to be wrong when you decide...
- But you get multiple chances to be unlucky
- I push for 99% confidence:
($p < 0.01)
Recap of A/B setup
- Develop two versions of a page
- Randomly divide users into two groups
- Show each group a different version
- Track how those users perform
- Evaluate the versions
- Go with the winning version
Recap of G-test evaluation

- Select a yes/no question about users
- Divide users in A and B into yes/no
- Perform complicated G-test calculation to calculate
$p - Our confidence is
1-$p - Make decision if our confidence is near 100% and we have enough samples
- Enough samples is at least 10 yes and no results in each test
What if I don't have Perl?

- Perl comes with virtually all forms of Unix, including OS X and Cygwin
- You can get a native Perl for Windows from http://strawberryperl.com
- With either solution you can get Statistics::Distributions
- In Unix:
perl -MCPAN -e 'install Statistics::Distributions' - In DOS:
perl -MCPAN -e "install Statistics::Distributions"
What if I don't want Perl?

- We all have JavaScript, right?
- I ported Statistics::Distributions to JavaScript
- statistics-distributions.js comes with this talk
- It is available on the same terms as Perl
- Which means the Artistic License, or GPL v1 or later
- It offers the same functions as the Perl version
Show Me

- Here is a Perl G-test Calculator for you
- And a JavaScript G-test Calculator for you
- I recommend installing these somewhere
- Point your product managers at the web version
- ...so they don't have to bug you when they want to play with hypothetical numbers
Tests are temporary

- Let's move on to considerations for developers
- Developers normally want maintainable code
- A/B testing calls for deletable code
- Normal code doesn't die
- A/B tests finish, one version wins, the others are deleted
- Then you write another test...
Streamline development

- You will write a lot of A/B tests
- Make the process as easy as possible
- Eliminate annoying steps
- Build a framework
- Automate reporting
Programming API

- You need a way to find what version a person gets
- Setting it if need be
- Should be self-documenting
- Needs to support some hidden functionality
- You will use this over and over again
A sufficient API
my $version
= get_or_create_test_version(
$person_id, "some test name",
["some version", "another version", ...],
[4, 1, ...] # optional, defaults to [1, 1, ...]
);
- This is enough, but a bit hackish
- Cleaner to add
get_test_version($person_id, $test_name); - In code you find the version, show the appropriate thing
- The optional argument gives relative frequencies
- That is a nice to have - you don't really need that
Behind the scenes

- The first time a person comes they are not found
- A random version is created, saved and returned
- The next time the previous version is found and returned
- So the random pick is permanent
Complications behind the scenes
- There are some complications to consider
- You want to use caching
- Need QA hook to set person into version (eg CGI parameter)
- Need production hook to, without a code release, cause a test to only return one specific version
- Production hook could be database entry, property file, etc
- This will be used to end tests
- It is also useful if there is a bug in a test
Code outline for function
sub get_or_create_test_version {
my ($person_id, $test, $versions, $weights) = @_;
}
Code outline for function
sub get_or_create_test_version {
my ($person_id, $test, $versions, $weights) = @_;
my $version = production_test_override($test)
|| get_test_from_cache($person_id, $test);
return $version if $version;
}
Code outline for function
sub get_or_create_test_version {
my ($person_id, $test, $versions, $weights) = @_;
my $version = production_test_override($test)
|| get_test_from_cache($person_id, $test);
return $version if $version;
$version = get_test_from_database($person_id, $test);
if (not $version) {
}
save_test_to_cache($person_id, $test, $version);
return $version;
}
Code outline for function
sub get_or_create_test_version {
my ($person_id, $test, $versions, $weights) = @_;
my $version = production_test_override($test)
|| get_test_from_cache($person_id, $test);
return $version if $version;
$version = get_test_from_database($person_id, $test);
if (not $version) {
# choose_random_version should NOT use $person_id
$version = qa_test_override($test)
|| choose_random_version($versions, $weights)
|| return;
save_test_to_database($person_id, $test, $version);
}
save_test_to_cache($person_id, $test, $version);
return $version;
}
Naming your tests

- Standardize your naming scheme
- Have ticket numbers in test names
- That avoids accidentally reusing names (which could mess up reporting)
- Also provides way to learn more more about a test
- Use self-explanatory test names
- Use self-explanatory version names
Naming example

- Test name: 1234-image-size
- Versions: thumb, full
- Ticket 1234 in Bugzilla should describe the A/B test
- The versions should mean what they say
In the database
- Only need one table
- Normalized tables require database patches, complicating development and deployment
- Necessary information:
person_id, test_name, version_name, creation_date - Primary key is
person_id, test_name - The creation date sometimes matters for reporting
Programming recap

- Use good test names, and include ticket numbers
- Setup and teardown of tests must be easy
- Make the programming API simple
- Behind the scenes need QA and production hooks
- Database design should be simple
Time for reporting
- We now have an A/B test running
- We know who is in which version of the test
- Now we need to know who did what we want
- But first, what did we want them to do?
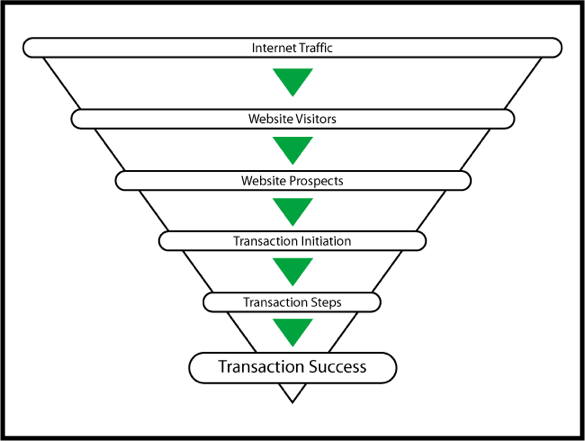
Your conversion funnel
- Every company has one or more conversion funnels
- You should know yours, and be actively trying to improve each step
- Each step can be tracked with some metric
- Most A/B tests concentrate on one step in the funnel
- Expect to run multiple A/B tests against each
- Standardize these metrics
Examples of metrics

- Sessions, sessions with registration
- People who searched, who viewed detail page, contacted, leased
- People who saved favorites, started a cart, completed purchase
- People who saw at least 3 pages, clicked on an ad
- Anything measurable and important to your business
Too many metrics?

- You may have many metrics
- High confidence on one may be chance
- Believe if it was the metric you tried to change
- Believe if very high confidence
- Believe if metrics agree
- Conflicting metrics require business decision
Reporting is work

- Developing reports takes time
- Running reports takes time, and interrupts programmers
- Run reports once a day, from cron
- Run a standard set of metrics against every A/B test
- Minimize custom reporting
Simplify custom reporting
log_test_activity(
$person_id, $test_name, $test_version, $action
);

- Many A/B tests need custom reporting
- Log the actions you want to report on
- Actions are things like "followed this link" or "hit this page"
- Have a cron job turn these logs into a set of metrics
- Takes care of most custom reporting needs
- Also good for registration tests
If you have a data warehouse

- A/B test results are slow to generate
- People often want to access them
- This is a perfect fit for a data warehouse
- For each metric, by test, by day entered the test, by day the activity happened, how many users entered that test the first day and became a yes on this metric for the second
- This summary is reasonably compact, and is very valuable
- Expect it to take a lot of time to set up
Is that it?

- You now know enough to run a successful A/B test!
- If you do everything right
- If you do it wrong you won't know
- You'll just get random answers
- And believe them
Compare apples to apples

- Traffic behaves differently at different times
- Friday night ≠ Monday morning
- First week in month ≠ last week in month
- Last week's visitors have done more than this week's
- Do not try to compare people from different times
Be careful when changing the mix

- A and B can receive unequal traffic
- But do not change the mix they get
- Wrong Change(90/10) A vs B to (80/20)
- You are implicitly comparing old A's with new B's
- Right Change(10/10/80) A vs B vs Untested to (20/20/60)
- This comes up repeatedly
What is wrong with this?

- Suppose you are A/B testing a change to your product page
- You log hits on your product page
- You log clicks on Buy Now
- You plug those numbers into the A/B calculator
- Is this OK?
Beware hidden correlations!

- Correlations increase variability, and therefore
$g_test - Some people look at many product pages
- Their buying behaviour is correlated on those pages
- This increases the size of chance fluctuations
- Leading to wrong results
Guarantee independence

- Whatever granularity (session, person, event) you make A/B decisons on...
- Needs to be what you test on
- In this case measure people who hit your product page
- Measure people who clicked on Buy Now
- Those are the right statistics to use
- This comes up repeatedly
People don't like UI changes

- A/B tests change how things work
- People may need time to adapt
- This can cause the new version to lose
- If you think this is likely to be an issue...
- Only enter new users into the test
- I can't predict how common this is
Schedule Compression

- Suppose you are A/B testing sending a reminder at 5 vs 10 days
- A does better than B for people between 5 days and 10 days
- This makes A look better than it is
- Solution: look at results for people who entered the test more than 2 weeks ago
- This comes up occasionally
Wrong metric
- At Rent.com we changed the title of our lease report email
- The new email had improved opens and clicks
- That was because it interested people who were still looking for a place to live
- That email needed to interest people who had already found a place to live
- We looked at the wrong metric, and it cost us millions
- This mistake is fairly rare
That's it!

- Those are the big mistakes that I've seen
- You now know how to do an A/B test
- ...and should have good odds of getting it right
- Of course there is more to know
- But this is the core
A simpler example

- We want to know how long A/B tests take
- We'll start with a simpler example
- Proving that a coin is not 50/50 heads/tails
- We have a test that a coin is fair
- Here is what an unfair coin might do
- Here is a longer look
Coin observations

- Errors happen early
- If chance and bias coincide, decide fast
- If they oppose, decide very, very slowly
- There is a very large range
A/B test simulation

- I ran multiple simulations of 100,000 parallel A/B tests
- Each simulation had a known real difference, and ran to a known confidence level
- Each step of the simulation added a person to A and B, then tested statistical significance
- Here are the results...
Best Case Example

- A's conversion rate: 55%
- B's conversion rate: 50%
- So 10% improvement on a good conversion rate
- Errors
- Completion
Low Conversion Example

- A's conversion rate: 11%
- B's conversion rate: 10%
- So 10% improvement on a bad conversion rate
- Errors
- Completion
Low Lift Example

- A's conversion rate: 51%
- B's conversion rate: 50%
- So 2% improvement on a good conversion rate
- Errors
- Completion
A/B test simulation conclusions

- Confidence does not mean odds of being right
- Mistakes are made early
- Time to finish is extremely variable
- 10,000 trials is enough for many useful A/B tests
- How long that takes depends on your website's volume
- Tests may take much, much longer than that
More conclusions

- Tests run faster with more volume
- Tests run faster with higher converting questions
- Your highest volume is at the top of the conversion funnel
- Your highest conversion is from one step to the next in the conversion funnel
- Plan your tests accordingly
Running multiple tests

- A/B tests can take a while to finish
- We have many A/B tests that we'd like to run
- It would be nice to not have to wait
- I have good news for you
- You DON'T have to wait!
Running multiple tests at once

- As long as people are randomly assigned to tests
- And no combination of test cases is really bad
- Each test's influence on the others is a random factor
- But there are other random factors (eg age, gender, income...)
- Doesn't matter to the statistics
Random assignment is essential

- The test version should be chosen with rand()
- Programmers often want to assign by $person_id mod 2
- That guarantees a perfectly even distribution of A and B
- But it also synchronizes one test with another
- Causing one test to affect the results of another
- You need those interactions to be random
Bad combinations are a lesser concern

- Test 1: displaying 24 vs 96 images at a time
- Test 2: displaying thumbnails vs larger pictures
- 96 larger pictures may be a bad experience
- So you wouldn't want to test these at the same time
- This kind of conflict is rare
Tip: Do many small tests

- Suppose you have 5 changes between A and B
- You will get one yes/no answer
- Some changes might be good, some bad, you have no insight
- 5 parallel tests is far more informative
- And finishes about as fast
A/B/C... testing the wrong way

- We often want to test more than 2 versions against each other
- Statistics books say g-test (and its relative chi-square) works for more than 2x2
- With
$nversions, and$mpossible answers, you can set up the table like we did... - do the same calculations (with more variables)...
- and
$p = chisqrprob(($n-1)*($m-1), $g_test)
Why is this wrong?

- The statistics books are right...
- but you can't interpret your answer!
- You know that there is a difference, but not what it is
- That's not good enough for us
- We need a winner
Extreme example

- Suppose we have 10 million versions
- Half convert at 51%, half at 49%
- At 21 samples each you know they are different
- But you can't tell the 51% versions from the 49% versions!
A/B/C... testing take 2

- Try to show that the best is better than the worst
- So compare the best with the worst using the g-test
- We get a probability
$pof our result for a random pair - But we expect the best and worst to be different
- So a low
$pis more likely than chisqrprob says - We need a fudge factor to correct
Finding the right fudge factor

- There are
$n*($n-1)/2pairs of versions - Therefore a low
$pcould happen this many ways - That's a lower bound on
$p - Let's verify by simulating a million A/B tests
- Here are the resulting graphs
$n*($n-1)/2is indeed a close estimate at the point where we want to make decisions
A/B/C... testing the right way

- Run your A/B test with
$nversions - Compare the best with the worst
- Multiply
$pby an appropriate fudge factor - If
$pis small enough, drop the worst version - Repeat until you have found your winner
Back to theory

- The G-test is a very powerful tool
- However there are things it can't do
- Plus we should look at a couple of things more deeply
- For that we need some more theory
Some basic terms

- Let
Xbe a random variable - The expected value,
E(X), is what you expect the arithmetic average of many samples to be - The variance,
Var(X), measures variability. It is defined asE((X - E(X))2) = E(X2) - E(X)2 - The standard deviation,
Std(X), issqrt(Var(X))
Distribution of the fair coin

- Let's consider the case of a fair coin
- Heads we call it 1, tails is 0
- The expected value is
0*p(0) + 1*p(1) = 0*0.5 + 1*0.5 = 0.5 - The variance is
(0-0.5)2*p(0) + (1-0.5)2*p(1) = 0.25*0.5 + 0.25*0.5 = 0.25 - The standard deviation is
sqrt(variance) = sqrt(0.25) = 0.5
Basic properties

- Let X and Y be independent random variables, and k be a constant
- Then the following hold
-
E(X+Y) = E(X) + E(Y), andVar(X+Y) = Var(X) + Var(Y) E(k+X) = k + E(X), andVar(k+X) = Var(X)-
E(k*X) = k * E(X), andVar(k*X) = k2 * Var(X)
Estimating E(X) and Var(X)

- Suppose
x1, x2, ..., xnare independent observations of a random variableX - Then the arithmetic average is an estimate of expected value
E(X) ≈ (x1 + x2 + ... + xn)/n - If
mis the arithmetic average
Var(X) ≈ (Σi=1n(xi - m)2)/(n - 1)
The normal distributions
- The standard normal is the classic "bell curve"
-
Statistics::Distributions and statistics-distributions.js tell
you everything you need to know about the standard normal with
udistr($p)anduprob($x). - There is a normal distribution for any given expected value and variance
- If
Xis a standard normal, thena+bXis a normal distribution with expected valueaand varianceb2 - Conversely if
Yis a normal distribution then(Y-E(Y))/Std(Y)is a standard normal
Central Limit Theorem
- Suppose
x1, x2, ..., xnare independent observations of a random variableX - Then
x1 + x2 + ... + xnhas approximately a normal distribution with expected valuen*E(X)and variancen*Var(X) - This is one of the most important theorems in math
- This is the most important theorem in statistics
- This is why people care about normal distributions
100 coin flips
- Let's return to the fair coin, with expected value 0.5, variance 0.25 and standard deviation 0.5
- If we flip it 100 times, we get approximately a normal distribution with expected value 50, variance 25, and standard deviation 5
- The odds of > 42.5 heads is
uprob((42.5-50)/5 = uprob(-1.5) = 0.93319 - 97.5% of the time you are
> udistr(0.975)*5 + 50 = 40.2 - 2.5% of the time you are >
udistr(0.25)*5 + 50 = 59.8 - The theoretical 95% confidence interval is
(40.2, 59.8), which is(40, 60)due to discreteness
Convergence to the mean
- What is the distribution of
(X1 + ... + Xn)/n? - Its expected value is
E(X)and its variance isn*Var(X)/n2 = Var(X)/n - It is approximately normal
- Here is its graph for the fair coin
- It takes 25 times as much data to make it 5 times as precise
- We saw that in comparing our best case and low lift examples
What is the Chi-square distribution?

- What is this
chisqrprob(1, $g_test)we've been using? - Suppose that
Xis a standard normal - Then
X2has a 1-dimensional Chi-square distribution - The sum of n independent 1-dim Chi-squares has the n-dimensional Chi-square distribution
chisqrprob(n, x)andchisqrdistr(n, p)describe the Chi-square distribution with n degrees of freedom
History of the G-test

- In 1900 Pearson came up with the G-test while studying log likelihood ratios
- He found its distribution
- He created the more conveniently calculated Chi-square test
- The Chi-square test is the same as the G-test, only with terms
of the form
($measured - $expected)2/$expected. - The Chi-square test was widely adopted
- The G-test is better
The Yates' continuity correction

- The G-test and chi-square tests err on the small side
- So we might end A/B tests too early
- Frank Yates suggested adjusting all measured values 0.5 towards the expected values
- ...because an ideal 40.2 vs 59.8 observation is really going to be 40 vs 60
- This correction improves accuracy slightly
How much money did we make?

- People often want to measure improvements in dollars
- They also want confidence ranges
- The G-test doesn't give either
- This can be frustrating
A/B Testing Setup
- Divide people into A and B
- Track them, figure how well each performed (eg revenue per person), including those who earned nothing
- That is our raw data
- How to analyze it?
First attempt, sidestep

- Often you can assume that the lift in conversion is proportional to dollars
- Not always true
- Particularly if you're testing directing more attention to your best customers
- Questions like, "How many are above __ (page views, dollars, etc)?" can address that
- Still not satisfactory
Second attempt, standard statistics

- We look in a statistics book
- And find that the t-test using the Student's t-distribution is meant to solve our exact problem, likewise ANOVA
- Unfortunately they only work if data is normally distributed
- Business data is not normally distributed
- Neither test is applicable
What does business data look like?
- In 1906 economist Vilfredo Pareto noted that 20% of the people owned 80% of of the wealth
- He found a family of power law distributions to describe this
- Pareto distributions turn up in many places such as individual wealth, size of cities, file sizes...
- size of sand particles, math papers published, areas burned by forest fires, bugs in modules, traffic on blogs...
- and one likely approximates the value of your customers
What about at the extreme?

- Pareto distributions lead to extremes
- The top samples follow Zipf's law
- Zipf's law says the n'th largest measurement is about 1/n times the size of the largest
- It turns up all over, including word frequency, book sales, photographs taken, lengths of rivers...
- and likely in the value of your top customers
Ignoring the extreme
- Statistics is not a good way to get to know these people
- Better would be dinner and a nice bottle of wine
- We may need to truncate the extremes away
- Choose a cutoff to truncate at
- Truncate everything above that cutoff to that cutoff before doing your statistics
Third attempt, z-test

- Define
mean(A)to besum(A)/count(A) - We saw that
mean(A)is approximately normal with varianceVar(A)/count(A) - Similarly
mean(B)is approximately normal with varianceVar(B)/count(B) mean(A) - mean(B)is approximately normal with varianceVar(A)/count(A) + Var(B)/count(B)
z-test cont.
(mean(A) - mean(B)) / sqrt(Var(A)/count(A) + Var(B)/count(B))
- If A and B have the same average, the above is approximately a standard normal
- We use our estimates of the variances of A and B
uprob($x)gives us the probability$p_largerthat a standard normal is greater than this number- Our confidence as a percentage is
200*abs(0.5 - $p_larger), you can also create confidence intervals for the difference - See the Perl utility z-test-example for an implementation
Limitations
- This assumes our estimate of the variance is correct
- This assumes the normal is a good approximation
- Define the variance weight of an observation to be the percent the estimated variance goes down if you take that observation out of the data set
- If the variance weight of the largest elements of A and B are both under 1%, the z-test is reasonably accurate
- Truncation may be necessary
Reconsider the G-test?

- The z-test works
- It is slower than the G-test
- It is more complicated than the G-test
- If you can, use the G-test instead
About this presentation
- All code and text, including the Perl utilities, simulations, statistics-distributions.js and the web G-test Calculator is available on the same terms as Perl
- The simulations were run with Perl, using Statistics::Distributions and the graphs were produced with gnuplot
- Many pictures are from Flickr and are under various licenses. Each is linked to its source. A number of them are not free for commercial use and have been included here with explicit permission.
- You are free to download this presentation and all supporting scripts, data files, etc in a single tar file
Questions?
 The next slides have some of the questions that came up during and after
the talk.
The next slides have some of the questions that came up during and after
the talk.
And there were questions
How long have you been doing A/B testing?I think my first A/B test was in late 2003. So nearly 5 years.
What organizational impacts are there?
A/B testing may be initially threatening to those who perceive themselves as experts. So do your best to have your first couple of A/B tests be fairly easy wins with the product manager on board. One you have financial results it is easier to handle people who don't like discovering that their pronouncements are not infallible.
What you refuse to see, is your worst trap has more to say on why people don't like these challenges.
And more questions
How do you budget the time for A/B testing?Generally the time to set up A/B tests comes out the regular development schedule. That is why I made such a big deal out of making it as lightweight as possible on the developers. There are a lot of demands on developers, and schedule pressure is one of them. You want to avoid having reasons to push back.
Currently my job is reporting. Reporting on A/B tests is one of my responsibilities. However if you don't have a dedicated person for reporting (we didn't when I first worked on A/B testing) then the time to develop reports will again come out of your development budget. Which is a good reason to try to reuse reporting from one project to another.
And more questions
What if we want to do this in Java?All of the code presented is easily written in any language, including Java, except for the call to chisqrdistr. My suggestion there is to get Rhino and then you can embed statistics-distributions.js in your Java program and call it. You only need to call one function.
For other languages you can set up a command line utility or a web service. Unless you want to port the utility again... If you want to port the library then I suggest starting with the JavaScript version. It is more consistently parenthesized so there will be fewer possible gotchas.
And more questions
What do you think of Google's Website Optimizer?If you want to get going on A/B testing and don't want to worry about doing any of the reporting, are concerned you'll get it wrong, etc, then by all means use it. However be aware that it has a number of major limitations. It works by using JavaScript to inject static content into your page. The fact that it is static makes it hard to have the bit that you're A/B testing be dynamic. You can do it, by having it inject some JavaScript that dynamically rewrites your HTML, but that is hackish.
There are other limitations. It doesn't support multiple metrics. It can't be used to A/B test email content.
If none of those are a problem for you, then by all means use it. However I think the flexibility of doing it yourself are worthwhile.
And more questions
What about A/B testing large pieces of functionality?You can A/B test anything. However with large projects it may not make sense during development to try to hide it behind an A/B test. In that case you could just release the project and then start A/B testing features within it.
Which way you go is up to you.
And a bug
How to calculate the fudge factor?Due to a bug in a simulation, I had calculated the fudge factors wrong for n-way chi-square and g-tests. My thanks to Lukas Trötzmüller for catching this many years later, and my apologies to people who relied on that mistake over the years.